SARSA (State, Action, Reward, next-State, next-Action)

Qu'est ce que le SARSA ?

SARSA est un algorithme d’apprentissage par renforcement on-policy, c’est-à-dire qu’il met à jour sa fonction de state-value $Q(s,a)$ en suivant exactement la politique utilisée pour agir. Contrairement au Q-Learning (off-policy), SARSA apprend en évaluant les actions réellement choisies, même lorsqu'il s'agit d'un choix aléatoire (exploration).

L’acronyme signifie :

• s : état actuel
• a : action choisie
• r : récompense reçue
• s’ : état suivant
• a’ : action suivante choisie par la même politique

La mise à jour est définie ainsi :

$$Q(s,a)\leftarrow Q(s,a)+\alpha [r+\gamma Q(s^{\prime },a^{\prime })-Q(s,a)]$$

Pourquoi utiliser SARSA ?

SARSA est particulièrement intéressant pour :

• apprendre à partir de l’expérience réelle dans l’environnement,
• gérer naturellement l’exploration via $ϵ$-greedy,
• conserver un comportement plus conservateur que Q-Learning (utile dans des environnements où des actions dangereuses mènent à des chutes rapides).

Comme il s’agit d’un algorithme on-policy, il évolue progressivement vers une politique sûre et performante tout en tenant compte des actions exploratoires.

Réalisation de l’algorithme

Dans cette implémentation, nous utilisons SARSA sur l’environnement CartPole-v1. Comme l’espace d’états est continu, nous devons le discrétiser avant l’apprentissage.

Variables initialisées :

• $Q(s,a)=0$ pour tout couple état-action
• $N(s,a)=0$ nombre de visites des couples
• $t=0$ time-step gobal (multi-épisodique)
• $\alpha =0.1$ alpha
• $ϵ=\frac{1}{t}$ apprentissage on-policy
• $\pi$ : $ϵ$-greedy sur $Q$

Structure générale du SARSA :

1. Observer $s$
2. Choisir $a$ selon $ϵ$-greedy
3. Exécuter $a$, recevoir $r$ et observer $s^{\prime }$
4. Choisir $a^{\prime }$ selon la même politique
5. Mettre à jour :

$$Q(s,a)\leftarrow Q(s,a)+\alpha \left[r+\gamma Q(s^{\prime },a^{\prime })-Q(s,a)\right]$$

6. Passer à $s\leftarrow s^{\prime }$, $a\leftarrow a^{\prime }$
7. Boucler sur les étapes 3 à 6 jusqu’à la fin de l’épisode

Implémentation

• Discrétisation en n_bins pour chaque variable de l’état
• Mise à jour SARSA pas à pas
• $\gamma =0.9$
• Exploration décroissante proportionnelle à $t$
• $ϵ$ $minimal=0.05$ (pas obligatoire pour l'algorithme)

Code utilisé

import gymnasium as gym
import random
import numpy as np

class SARSA:
    def __init__(self, alpha=0.1, gamma=0.9, n_bins=10):
        self.q = {}
        self.alpha = alpha
        self.gamma = gamma
        self.bins = {
            'cart_pos': np.linspace(-2.4, 2.4, n_bins),
            'cart_vel': np.linspace(-3.0, 3.0, n_bins),
            'pole_angle': np.linspace(-0.21, 0.21, n_bins),
            'pole_vel': np.linspace(-3.5, 3.5, n_bins)
        }

    def get_q(self, s, a):
        return self.q.get((s, a), 0.0)

    def choose_action(self, state, epsilon):
        if random.random() < epsilon:
            return random.randint(0, 1)
        state_disc = self.discretize(state)
        return np.argmax([self.get_q(state_disc, a) for a in [0, 1]])

    def discretize(self, state):
        state = np.clip(state, [-2.4, -3.0, -0.21, -3.5], [2.4, 3.0, 0.21, 3.5])
        b = [
            np.digitize(state[0], self.bins['cart_pos']),
            np.digitize(state[1], self.bins['cart_vel']),
            np.digitize(state[2], self.bins['pole_angle']),
            np.digitize(state[3], self.bins['pole_vel'])
        ]
        return tuple(b)

    def learn(self, s, a, r, s_next, a_next):
        s = self.discretize(s)
        s_next = self.discretize(s_next)
        q_next = self.get_q(s_next, a_next)
        old_q = self.get_q(s, a)
        self.q[(s, a)] = old_q + self.alpha * (r + self.gamma * q_next - old_q)


env = gym.make("CartPole-v1")

alpha = 0.1
gamma = 0.9
nb_bins = 10
agent = SARSA(alpha=alpha, gamma=gamma, n_bins=nb_bins)
epsilon = 1.0
epsilon_min = 0.05
t = 0

for episode in range(20000):
    state, _ = env.reset()
    action = agent.choose_action(state, epsilon)
    total = 0
    done = False

    while not done:
        t += 1

        if epsilon > epsilon_min:
            epsilon = max(1 / t, epsilon_min)

        next_state, reward, terminated, truncated, _ = env.step(action)
        done = terminated or truncated
        next_action = agent.choose_action(next_state, epsilon)

        agent.learn(state, action, reward, next_state, next_action)

        state, action = next_state, next_action
        total += reward

    print(f"Episode {episode+1}, score: {total}, epsilon={epsilon:.2f}")

env.close()

Itérations avec plusieurs paramêtres

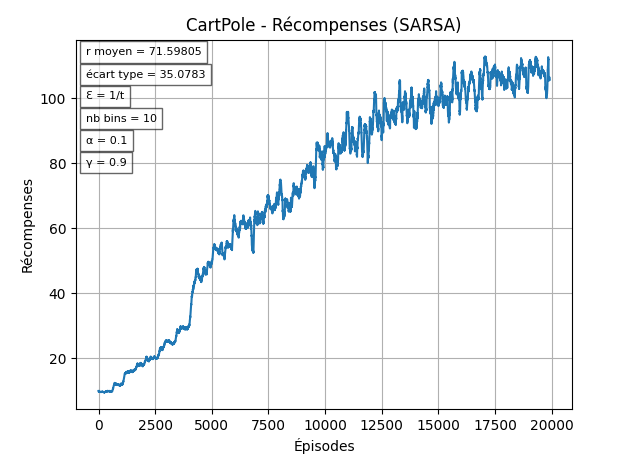
Avec $ϵ$ = 1/t et $\alpha$ constant

Avec les paramêtres "par défaut", les résultats obtenus sont assez faibles comparés au reward maximal de 500. C'est notamment dû au fait que $ϵ$ diminue très vite.

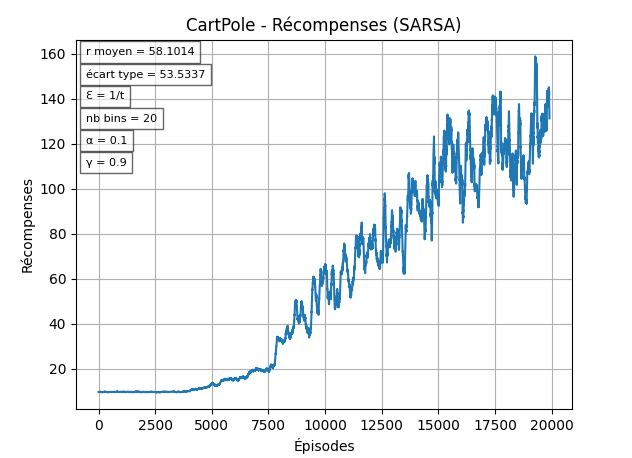
Remarque sur la discrétisation

Pour cet environnement, la "résolution" (le nombre de bins) idéal pour les variables d'état semble être entre 15 et 25. On utilisera donc 20 bins pour les prochains tests:

Alpha Dynamique

Ensuite, on veut que le taux d'apprentissage général ($\alpha$) évolue au fil des épisodes pour donner plus d'importance à la politique apprise au bout d'un certains temps (sinon on risque de stagner / être ralentit à cause des choix exploratoires).

$$\alpha =\frac{1}{t}$$

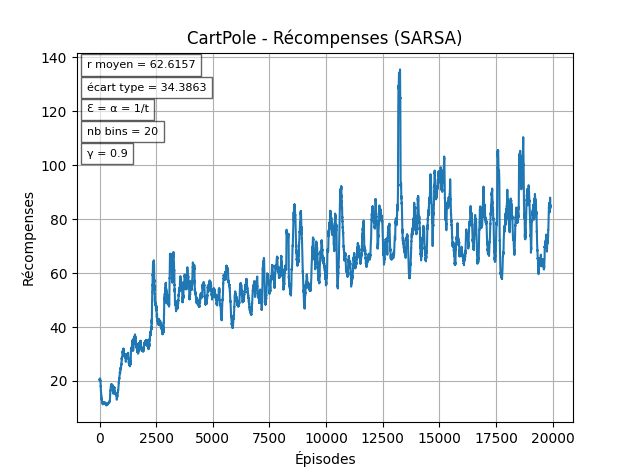
On peut observer ici que l'agent arrive un peu plus vite à des rewards "stables".

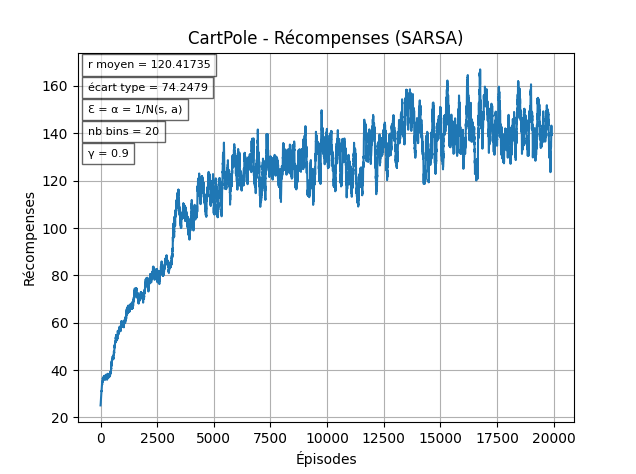
En utilisant N(s, a)

Maintenant, on a une phase majoritairement d'exploration, et une autre pour l'exploitation, mais on continue de diminuer nos chances d'explorer sans regarder si on a déjà une "bonne" politique pour l'état. Pour remédier à ça, on va modifier nos chances selon le nombre de visites de la paire $(s,a)$:

$$ϵ=\frac{1}{N(s,a)}\alpha =\frac{1}{N(s,a)}$$

Cette solution permet d'avoir une décroissance de l'exploration qui est spécifique à chaque paire $(s,a)$.

En utilisant la racine carrée de N(s, a)

Avec $\sqrt{N(s,a)}$ on permet à l'agent d'explorer un peu plus, ce qui affecte grandement les résulats. Comme on peut le voir ci-dessous, il est commun que l'agent s'approche de la politique optimale, mais cela dépend encore beaucoup de l'aléatoire durant les 2000 premiers épisodes.

$$ϵ=\frac{1}{\sqrt{N(s,a)}}\alpha =\frac{1}{\sqrt{N(s,a)}}$$

Meilleur essai sur 20 tentatives:

Contre-exemple:

Conclusion

En résumé, SARSA est un algorithme robuste mais fortement sensible à l’initialisation stochastique : les premiers épisodes jouent un rôle déterminant, et un bon mécanisme de gestion de l’exploration (comme une décroissance dépendant des visites) peut faire toute la différence entre un apprentissage lent et la convergence vers une politique optimale.