Monte Carlo Online Control on Policy improvement (MCOC on P-imp)
Qu'est ce que le Monte Carlo Online Control (MCOC) ?
Le Monte Carlo online control est un algorithme, qui à partir des résultats récoltés, améliore la politique de jeu actuelle, dans le but de trouver la meilleure possible.
Pourquoi utiliser le MCOC ?
Cet algorithme est très utile pour apprendre une politique optimale à partir des intéractions avec l'environnement, car il se base sur son expérience. Cet algorithme est simple et possède un équilibre entre exploration et exploitation, il explore la plus part du temps l'action la plus optimate, mais explore de temps en temps d'autres actions selon .
Réalisation de l'Algorithme
Pour réaliser cet algorithme, nous commençons par initialiser les données suivants : ou
- s correspond à l'état
- a correspond à l'action
- Q (s, a) correspond à la valeur d'un état en effectuant une action, et en suivant la politique
- N (s, a) correspond au nombre de visite
- correspond aux taux d'explorations dans la politique -greedy
- correspond à la politique utilisée
- k correspond au compteur d'épisode
Utilisation de l'algorithme sur CliffWalking-v1
Nous avons utilisé cet algorithme sur l'environnement gymnasium CliffWalking afin de trouver le chemin le plus optimale, et voici le résultat obtenu :
Code de l'algorithme
import gymnasium as gym
import numpy as np
from scipy.signal import lfilter
import math
from collections import defaultdict
class MCOC:
def __init__(self, env, gamma, epsilon):
self.env = env
self.gamma = gamma
self.epsilon = epsilon
self.q_values = defaultdict(float)
self.n_visits = defaultdict(int)
self.policy = {}
self.num_actions = env.action_space.n
self.num_states = env.observation_space.n
self.episodes = []
self.p = []
def get_q(self, s, a): return self.q_values.get((s, a), 0.0)
def get_n(self, s, a): return self.n_visits.get((s, a), 0.0)
def get_policy(self, s, a): return self.policy.get((s, a), 0.0)
def choose_action(self, p):
return np.random.choice(range(self.num_actions), p=p)
def best_action(self, state):
return max(range(self.num_actions), key=lambda a:self.get_q(state, a))
def evaluate(self, state, action, i, G):
self.n_visits[(state, action)] = self.get_n(state, action) + 1
#self.q_values[(state, action)] = self.get_q(state, action) + (math.sqrt(1 / self.get_n(state, action)) * (G[i] - self.get_q(state, action)))
self.q_values[(state, action)] = self.get_q(state, action) + (1 / self.get_n(state, action) * (G[i] - self.get_q(state, action)))
def epsilon_greedy(self, state):
best_action = self.best_action(state)
p = np.full(self.num_actions, self.epsilon / self.num_actions, dtype=float)
p[best_action] += 1.0 - self.epsilon
for action in range(self.num_actions):
self.policy[(state, action)] = p[action]
return p
def update_visits(self, episodes):
visited = set()
for t, (s, action, reward) in enumerate(episodes):
# if first visit
if (s, action) not in visited:
agent.evaluate(s, action, t, G)
visited.add((s, action))
return visited
def upgrade_policy(self):
for state in range(self.num_states):
agent.epsilon_greedy(state)
env = gym.make("CliffWalking-v1")
epsilon = 1
k = 1
gamma = 0.9
num_episodes = 150000
agent = MCOC(env=env, gamma=gamma, epsilon=epsilon)
visited = set()
#loop
for episode in range(num_episodes):
if episode % 1000 == 0:
print("Episode:", episode)
state, _ = env.reset()
finish = False
visited = set()
#sample k-th episode given pi_k
while not finish:
p = agent.epsilon_greedy(state)
action = agent.choose_action(p)
next_state, reward, terminated, truncated, _ = env.step(action)
agent.episodes.append((state, action, reward))
state = next_state
finish = terminated or truncated
#Gkt
T = len(agent.episodes)
rewards = np.array([r for (_, _, r) in agent.episodes])
G = lfilter([1], [1, -gamma], rewards[::-1])[::-1]
#for t= 1..T do
visited = agent.update_visits(agent.episodes)
agent.episodes = []
k += 1
agent.epsilon = max(1 / k, 0.05)
#agent.epsilon = 1 / k
#pi_k = epsilon-greedy(Q)
agent.upgrade_policy()
Données utilisées :
Les essais
Nous avons réalisé les essais, et en faisant entre 150 000 et 400 000 episodes, nous obtenons toujours le même rewards, qui est égale à -17.
Conclusion
Il faut effectuer encore des millions d'episodes afin que l'agent puisse tout explorer et trouver la meilleur politique possible, qui donnerait le schéma suivant :
Utilisation de l'algorithme sur Cartpole-v1
Pour utiliser l'algorithme sur cartpole-v1, Nous avons du discretiser l'espace des etats de l'environnement avec une intervalle de 12 car Cartpole possède des états continus, alors que le MCOC nécessite des états discret.
Cartpole-v1 nous fournit les informations suivant :
- Position du chariot : de -4.8 à 4.8
- Vitesse du chariot : -∞ à +∞
- Angle du pôle : −0.418 rad à +0.418 rad
- Vitesse angulaire du pôle : −∞ à +∞
Code de l'algorithme :
def create_bins(num_bins=6):
return [
np.linspace(-4.8, 4.8, num_bins), # position
np.linspace(-5, 5, num_bins), # vitesse
np.linspace(-0.418, 0.418, num_bins), # angle
np.linspace(-5, 5, num_bins) # vitesse angulaire
]
bins = create_bins()
def discretize(state):
return tuple(int(np.digitize(s, b)) for s, b in zip(state, bins))
def MCOC(gamma, num_episodes):
env = gym.make("CartPole-v1")
# 6 bins par dimension → 6^4 = 1296 états
num_states = 6 ** 4
num_actions = env.action_space.n
k = 1
epsilon = 1
Q_values = np.zeros((num_states, num_actions))
N_visits = np.zeros((num_states, num_actions))
policy = np.ones((num_states, num_actions)) / num_actions
# --- MAIN LOOP ---
for g in range(1, num_episodes + 1):
episodes = []
rewardepisode = 0
state_cont, info = env.reset()
state = get_index(discretize(state_cont))
while True:
# best action
best_action = np.argmax(Q_values[state, :])
# remplir proba
for a in range(num_actions):
if a == best_action:
policy[state, a] = 1 - epsilon + (epsilon / num_actions)
else:
policy[state, a] = epsilon / num_actions
p = policy[state]
p = p / p.sum()
action = np.random.choice(range(num_actions), p=p)
next_state_cont, reward, terminated, truncated, _ = env.step(action)
rewardepisode += reward
next_state = get_index(discretize(next_state_cont))
episodes.append((state, action, reward))
if terminated or truncated:
break
state = next_state
# --- Monte Carlo return ---
G = {}
T = len(episodes)
G[T - 1] = episodes[T - 1][2]
for t in range(T - 2, -1, -1):
G[t] = episodes[t][2] + gamma * G[t + 1]
# --- First Visit MC ---
visited = set()
for t, (state, action, reward) in enumerate(episodes):
if (state, action) not in visited:
visited.add((state, action))
N_visits[state, action] += 1
alpha = math.sqrt(1 / N_visits[state, action])
Q_values[state, action] += alpha * (G[t] - Q_values[state, action])
# --- Policy Improvement ---
k += 1
epsilon = 1 / k
for s in range(num_states):
best_action = np.argmax(Q_values[s, :])
for a in range(num_actions):
if a == best_action:
policy[s, a] = 1 - epsilon + (epsilon / num_actions)
else:
policy[s, a] = epsilon / num_actions
print(g , rewardepisode)
return Q_values, policy
# --- Convertit un tuple d'indices (ex: (3,2,1,4)) en un index unique 0..1295 ---
def get_index(indices, num_bins=6):
i0, i1, i2, i3 = indices
return i0 * num_bins**3 + i1 * num_bins**2 + i2 * num_bins + i3
Données utilisées :
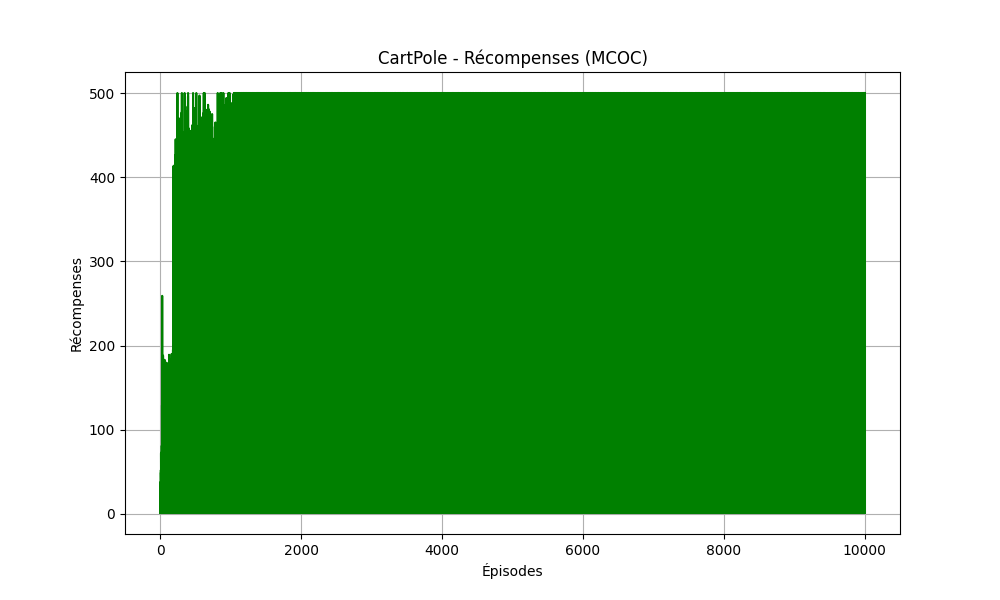
Essai et Résultat
Nous avons effectué un test de 10 000 episodes sur cartpole avec cet algorithme, et cela fût un front succès. L'algorithme a atteint le reward maximal à atteindre (500), comme on peut le voir dans le graphique en dessous, l'algorithme a été constant, du 1000 ème episode jusqu'à la fin.
