Processus de Markov
théorique
Explication "global" du MP
Un processus de Markov est un processus stochastique dans lequel la prédiction du futur ne dépend que de l’état présent. Autrement dit, connaître les états passés ne rend pas la prédiction du futur plus précise : seul l’état actuel compte.
MP est défini par une fonction :
- S : Un ensemble d'état fini
- P : Une matrice de transition des probabilités
P : S -> [0, 1]
s, P(s,s') = 1
S : Un nombre fini d'états St : Un état défini par un temps t
pour simplifier, on a une fonction qui prend comme arguments s et s' et donne la probabilité de passer de l'état s à l'état s' on l'apelle Transition Probability Function.
La matrice de transition :
Si l’ensemble des états étant fini, on peut regrouper toutes les probabilités de transition dans une matrice de transition (P) :
Explication "détaillée" du MP
Une chaîne de Markov sur un est une suite de variables aléatoires à valeurs dans telle que pour tout : Remarque : le seul degré de liberté d'une chaîne est donc dans sa loi initiale .
1. Propriété de Markov
source: wikipédia (attention hyper complexe)
t 0,
Avant les explications, il est à noter qu'il y a plusieurs types de propriétés de Markov, chacune dans des ensembles différents ou avec des conditions différentes. Nous allons nous intéresser à la propriété de Markov dite "faible" (temps discret, espace discret) car c'est celle qui est la plus compréhensible et la plus utilisée.
On dit qu’un processus vérifie la propriété de Markov si :
En GROS le futur ne dépend que du présent, les états dans lesquels nous avons été sont inutiles et n'affectent rien.
2. Exemple
Par exemple, la météo :
Supposons :
- S'il fait soleil aujourd’hui, il y a 50% de chances que demain il fasse encore soleil, 15% qu'il pleuve et 35% qu'il fasse nuageux.
- S’il pleut, il y a 60% de chances que demain il pleuve encore, 25% qu'il y ait des orages et 15% qu'il y ait des nuages.
- S'il il y a orages aujourd’hui, il y a 10% de chances que demain il fasse ensoleillé, 40% qu'il pleuve, 20% qu'il fasse encore orageux et 30% qu'il fasse nuageux.
- S'il fait nuageux aujourd’hui, il y a 10% de chances que demain il fasse ensoleillé, 10% qu'il pleuve et 80% qu'il fasse encore nuageux.
Alors :
les états passés sont inutiles, seul ceux du présent comptent pour connaître les états futurs
3. Représentation par un graphe orienté
On peut représenter la chaîne sous forme de graphe où :
- les nœuds = les états
- les arcs = les transitions
- les poids = probabilités de transition
L'exemple précedent donnerais alors :
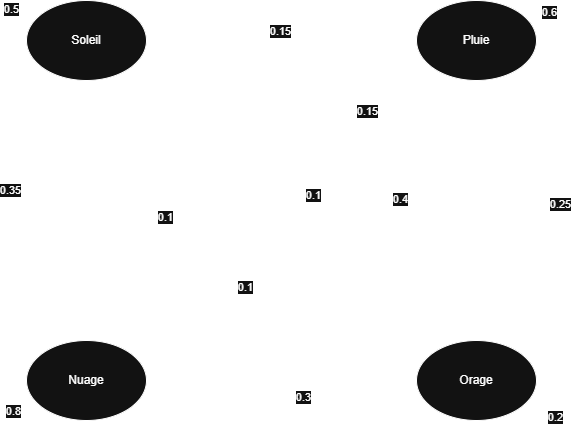
Un MP est irréductible si le graphe de est fortement connexe. Il est apériodique si sa période est égale à 1.
4. État stationnaire
Un processus de Markov converge parfois vers une distribution stationnaire = , ..., est telle que :
Une distribution stationnaire est une distribution de probabilités sur les états qui reste inchangée au fil du temps.
Informellement, au départ l’état dépend de là où on démarre, mais à force de répétition les probabilités s'affinent et arrivent à un état de distribution stable
Conclusion
Un processus de Markov est donc un modèle où l’évolution ne dépend que de l'état actuel. Les probabilités de transition peuvent être regroupées dans une matrice et permettent d’étudier le comportement du système à long terme.